这个是维基百科上的一段代码，经试验可以解数独。

链接：https://zh.wikipedia.org/wiki/Clojure#cite_note-:8-7

(def board
  [[0 2 0 0 0 5 0 0 7]
   [0 8 0 2 0 4 0 0 0]
   [7 0 0 0 0 0 0 0 6]
   [0 0 7 0 1 0 0 3 0]
   [9 0 0 0 5 0 0 0 0]
   [0 0 5 0 0 0 2 7 0]
   [0 0 0 1 0 7 6 8 0]
   [0 0 0 0 9 0 0 0 2]
   [0 0 0 6 0 3 7 5 0]])

(defn board-rows [board]
  (let [full-set (set (range 1 10))
        exists (mapv #(remove (partial == 0) %) board)]
    (mapv #(clojure.set/difference full-set (set %)) exists)))

(defn board-cols [board]
  (let [board-v (for [i (range 9)]
                  (map #(% i) board))]
    (board-rows board-v)))

(defn board-blks [board]
  (let [board-b (for [i (range 3)
                      j (range 3)]
                  (for [k (range 3)
                        l (range 3)
                        :let [x (+ k (* i 3))
                              y (+ l (* j 3))]]
                    (get-in board [x y])))]
    (board-rows board-b)))

(defn board-tofill [board]
  (vec (for [i (range 9)
             j (range 9)
             :let [v (get-in board [i j])]
             :when (== v 0)]
         [i j])))

(defn blk-ix [x y]
  (let [i (quot x 3)
        j (quot y 3)]
    (+ j (* i 3))))

(defn fill-cand [x y rows cols blks]
  (let [row (get rows x)
        col (get cols y)
        blk (get blks (blk-ix x y))]
    (clojure.set/intersection row col blk)))

(defn solve-sudoku
  ([tofill rows cols blks board]
     (if (empty? tofill)
       board
       (let [cands (for [i (range (count tofill))
                         :let [[x y] (get tofill i)
                               cand (fill-cand x y rows cols blks)]]
                     [i x y cand])
             [mk x y min-cand] (apply min-key #(count (peek %)) cands)
             tofill-update (vec (concat (take mk tofill) (drop (inc mk) tofill)))
             ]
         (when (not (empty? min-cand))
           (apply concat
                  (for [cand min-cand
                        :let [cand-set #{cand}
                              remove-cand (fn [s i] (update-in s [i] #(clojure.set/difference % cand-set)))
                              rows-update (remove-cand rows x)
                              cols-update (remove-cand cols y)
                              blks-update (remove-cand blks (blk-ix x y))
                              board-update (assoc-in board [x y] cand)
                              ]]
                    (solve-sudoku tofill-update rows-update cols-update blks-update board-update))))
         )))
  ([board]
     (let [tofill (board-tofill board)
           rows (board-rows board)
           cols (board-cols board)
           blks (board-blks board)
           ]
       (remove nil? (solve-sudoku tofill rows cols blks board))
       )))

(solve-sudoku board)

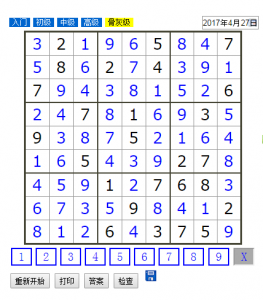
测试结果：

([3 2 1 9 6 5 8 4 7]
[5 8 6 2 7 4 3 9 1]
[7 9 4 3 8 1 5 2 6]
[2 4 7 8 1 6 9 3 5]
[9 3 8 7 5 2 1 6 4]
[1 6 5 4 3 9 2 7 8]
[4 5 9 1 2 7 6 8 3]
[6 7 3 5 9 8 4 1 2]
[8 1 2 6 4 3 7 5 9])

 

数独链接：http://cn.sudokupuzzle.org/